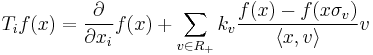Dunkl operator
In mathematics, particularly the study of Lie groups, a Dunkl operator is a certain kind of mathematical operator, involving differential operators but also reflections in an underlying space.
Formally, let G be a Coxeter group with reduced root system R and kv a multiplicity function on R (so ku = kv whenever the reflections σu and σv corresponding to the roots u and v are conjugate in G). Then, the Dunkl operator is defined by:
for 1 ≤ i ≤ N, x in RN, and f a smooth function on RN.
Dunkl operators were introduced by Dunkl (1989). One of Dunkl's major proofs was that Dunkl operators "commute," that is, they satisfy 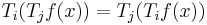 just as partial derivatives do. Thus Dunkl operators represent a meaningful generalization of partial derivatives.
just as partial derivatives do. Thus Dunkl operators represent a meaningful generalization of partial derivatives.
References
- Dunkl, Charles F. (1989), "Differential-difference operators associated to reflection groups", Transactions of the American Mathematical Society 311 (1): 167–183, doi:10.2307/2001022, ISSN 0002-9947, MR951883